これは、本文「重力蓄電装置の力学的考察(→)」の続編です。「重力蓄電装置の力学2(→)」でその理論的な部分を解説しましたが、ここでは実験上の注意や結果などの実践的な面を述べます。装置の構造その他の概要は、「本文」を参照して下さい。用語や記号もそれに従います。
重力を用いた蓄電方法は、外部電力によって重りを上部に吊り上げてその電力をポテンシャルエネルギーとして重りに蓄えておき、電力が必要になったときそれを落下させて再び電力を得るものです。したがって、重りの落下運動によって発電機を回すので、その力学的側面をじゅうぶん理解しておく必要があります。理論だけでは予想もつかない事実が、実験によって観察されます。
1. 負荷定数
重量 \(m\) の重りが、発電機を回しながら落下するとき、その落下速度 \(v\) は次式できまります。
\[ \tag{1} v = \frac{mg}{K}(1 - e ^{-\frac{K}{m}t}) \]この式についての詳細は、「重力蓄電装置の力学2」を参照して下さい。この式より、重りは最終的に殆んど速度 \(v = mg/K\) の等速度運動となります。ここで定数 \(K\) は、重りが落下するときに受ける抵抗の大きさの目安となる値で、発電機からの抗力と増速機のギア摩擦などできまります。この値は実験において重要な量となるので、「負荷定数」 と呼びます。
この重りを高さ \(l\) の位置から落としたとき、床面に達するまでの時間(落下時間)\(t_0\) は \(K\) が重量 \(m\) に比べて大きいとき、つぎのように表せます。
\[ \tag{2} t_0 = \frac{Kl}{mg} \]この近似については、「重力蓄電装置の力学2」に述べてあります。この式から、負荷定数 \(K\) は \(K = (mg/l)t_0\) とかけて、落下時間 \(t_0\) を測定すれば求められます。この \(t_0\) や \(K\) の値は、外部回路にかけた負荷抵抗の値の影響を受けます。発電機の容量にもよりますが、外部抵抗 \(R\) が小さければその回路には大きな電流が流れます。このとき、発電機には大きな機械的負荷がかかり、回転数は下がります。結果として、 \(K\) の値は大きくなります。
これは、定量的にはつぎのように説明できます。発電機の起電力を \(E\) で、そのとき回路に流れる電流を \(I\) とすれば、発電機のなす仕事率(電力) \(P\) は、 \(P = EI = I^2R\) とかけます。一方、初めの重りに蓄えられたポテンシャルエネルギー \(mgl\) がすべて発電にまわされたとして、 \(mgl = Pt_0\) が成り立ちます。これより、(2)式を用いて、\(K\) はつぎのように表せます。
\[ \tag{3} K = \frac{m^2g^2}{P} = \frac{m^2g^2}{I^2R} \]小容量の発電機の場合、外部抵抗による電流の変動は小さく、(3)式により \(K\) は殆んど \(R\) に反比例するように減少します。しかし、発電機の容量が大きいときは \(R\) の値が小さいほど大きな電流が流れ、 \(K\) の変動自体は少なくなります(表1を参照)。
以下に、実際の実験結果を述べます。これは、\(m\) = 106 (kg)、 \(l\) = 130 (cm) で、増速機のギア比は \(k\) = 100 (倍) で実験しました。負荷定数 \(K\) は、 \(K = (mg/l)t_0\) で求めました。外部抵抗値 \(R\) は抵抗器の目盛であって、正しい測定値ではありません。
表1
| \(R\) (Ω) | \(t_0\) (s) | \(E\) (V) | \(I\) (A) | \(P\) (W) | \(K\) |
| 10 | 9.6 | 24.9 | 1.98 | 49.3 | 7671 |
| 20 | 9.0 | 35.9 | 1.45 | 52.1 | 7192 |
| 50 | 8.0 | 53.6 | 0.98 | 52.5 | 6393 |
| 100 | 7.7 | 63.1 | 0.69 | 43.5 | 6153 |
| 200 | 7.9 | 86.0 | 0.43 | 37.0 | 6313 |
2. 初期動作
重りを落として発電機を起動させる際に、注意しなければならない多くの事があります。まず、重りを吊り下げた状態から解放するとき、引き金装置が必要となります。ここで、一般に回転軸における回転数とトルク(回転力)は反比例の関係にあることを利用します。増速機のギア比が大きければ、プーリーにかかるトルクは大きくなり、したがって重量の大きい重りを吊り上げられます。一方、増速機の発電機側は回転数が大きいので小さなトルクが働きます。そこで、発電機側にブレーキを装備し、それを閉じて重りを固定します。起動の際にそれを開放させれば、重りはゆっくり落下していきます。滑らかに落下させるにはガイドも必要となります。また、起動のときの重りにかかる衝撃力はかなり大きく、注意を要します。
自己励磁方式の交流発電機の場合、正常な発電が行われるまで時間がかかります。それは、初めのローターの回転で生じた交流電流を整流器により直流にして、再びローターに戻して励磁する方法をとっているからです。したがって、初め軽やかに回転していた発電機が、自己励磁状態になった途端に回転が重くなり、スティターに発生する電圧が急激に大きくなります。このとき、機械的かつ電気的な衝撃が起こる場合があります。この現象が起こる原因は、整流器に使われているダイオードの特性にあるように思われます。すなわち、ダイオードの両端にかかる電圧が一定以上になると、整流された電流が急に増加するからです。参考のために、オルタネーター発電機による、初期の出力電圧が確立していく様子を図1に示しました。これはオシロスコープで描いたものです。
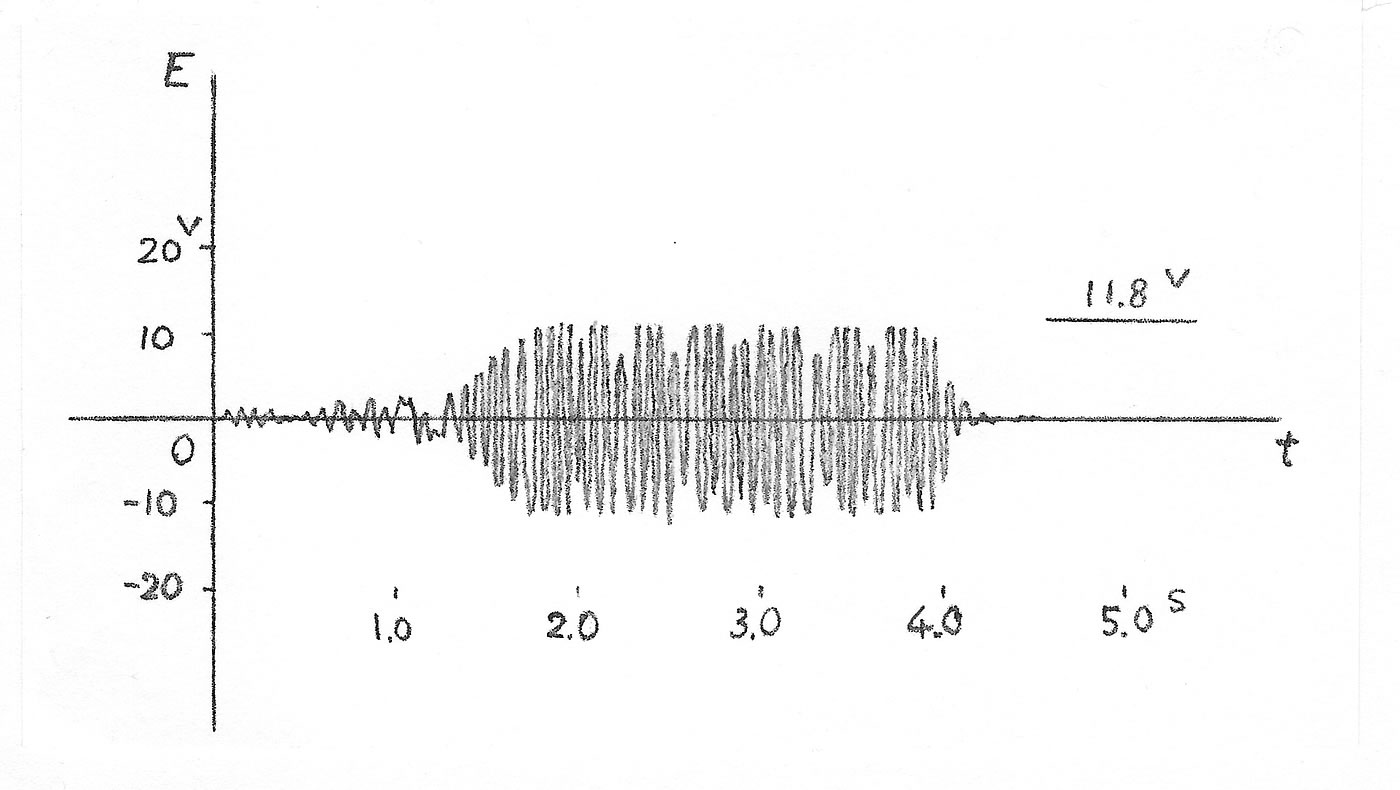
図1.起動時における起電力の確立
3. パラメーターバランス
装置の外部から制御できるパラメーターは、増速機のギア比 \(k\) とプーリーの直径 \(d\) および重りの重量 \(m\) です。高さ \(l\) も変更可能ですが、 \(l\) が大きいと落下時間は延びますが、実験のデーターをとるという立場からすれば、これは重要ではありません。問題はこれら3つのパラメーターのバランスです。出力を大きくするにはこれらの組み合わせが大切なのですが、今のところ明確な解答はありません。実験によってそれらを調整するしかないようです。そこで得られた結果を、以下に述べます。
システムが起動して、重りの落下が安定速度 \(v = mg/K\) に達したときの発電機の回転数 \(G\) は、(2)式を用いて、つぎのようになります。
\[ \tag{4} G = \frac{kl}{{\pi}dt_0} = \frac{kg}{{\pi}Kd}m \]この式から分かるとおり、回転数 \(G\) を上げるには重量 \(m\) を増やしてプーリーの径 \(d\) を小さくすればよいのですが、これでは落下時間が短くなり、期待される程の出力は得られません。出力は発電機の回転数だけではきまらず、そのトルクにも依存するようです。実際に、回転数が殆んど同じ2つの実験結果を比較してみます(表2参照)。
回転数とトルクは、同一軸ではギアの倍率によって、反比例の関係になります。初め、プーリーに与えられるトルクは \(T = md/2\) ですが、回転数がギア比 \(k\) によって \(k\) 倍されれば、発電機には \(T_G = md/(2k)\) のトルクが働きます。そこで、つぎの2つの場合を比べてみます。 \(d\) = 13.3 (cm)、 \(l\) = 130 (cm)、 \(R\) = 10 (Ω) は両実験において共通です。
表2
| \(k\) | \(m\)(kg) | \(t_0\)(s) | \(G\)(r/s) | \(T_G\)(kg·cm) | \(E\)(V) | \(I\)(A) | \(P\)(W) |
| 48 | 90 | 5.0 | 29.9 | 12.5 | 32.8 | 3.19 | 104.6 |
| 100 | 98 | 9.8 | 31.7 | 6.5 | 16.7 | 1.78 | 29.7 |
この表で、発電機の回転数はどちらも殆んど \(G\) = 30 (r/s) 前後なのですが、出力が全く異なります。これは、発電機に与えられたトルク \(T_G\) の違いによるものと思われます。すなわち大きい出力を得るには、発電機内部の磁界のつくる抗力に対抗するため、大きなトルクが必要になってくるのだと考えられます。またギア比を倍増すると、落下時間は延びますが出力は下がります。このとき、(3)式によって、負荷定数 \(K\) は倍増します。
4. 実験上の注意
出力を調べるには、外部回路に負荷抵抗をかけて、それに流れる電流と電圧を測定します。その際に、抵抗値が小さいときは大きな電流が流れるので注意が必要です。とくに、回路を短絡状態にして測定するのは危険が伴います。一方、開放状態では電圧が最高値に達するので、これも注意を要します。また、重りの重量に対してギア比が小さいときは落下時間が短くなり、出力は大きくなりますが、床面への衝撃が大きくこれも危険です。重りの重量とギア比のバランスは、事故を回避するためにも、大切です。
使用する発電機の励磁方式にも注意を払う必要があります。大型のものは、副励磁機と電圧調整器で磁界の強さを制御しているようですが、小型のものでは電圧調整のためにコンデンサーを使っているものが多いようです。この場合、コンデンサーへの充電放電の繰り返しのために、初めのうちは出力が不安定になることがあります。これはおそらく外部パラメーターのバランス、とくにトルクの不足が原因と思われます。
どんな発電機を使うかによりますが、それに合う外部制御のパラメーターを設定するのが重要です。これらのパラメーターは微妙に関連し合っていて、よい出力を得るには、試行錯誤によってベストな組み合わせを見つけるしかありません。また、トルクや回転数などの各量を計算式を用いて予測し、それを基にして装置の設計や実験をするのが望ましいと思います。これは、思わぬ事故を防ぐためにも必要なことです。
2019 年 2 月